Przykłady
Przykład 1
Rozważmy najprostszy przypadek funkcji $ f(x)$: $ \mathbb{R} \rightarrow \mathbb{R}$. Należy pamiętać, że aby istniała funkcja odwrotna $ g(y)$, taka że $ g(f(x))=x$ dla $ x\in \mathbb{R}$, to należy rozważać takie podzbiory $ \mathbb{R}$, na których $ f$ jest bijekcją. Weźmy dla przykładu funkcję: $$ f(x)=(x^2-16)^2,$$ której wykres pokazano na rysunku poniżej. Z wykresu widać, że funkcja $f$ nie jest bijekcją na całym zbiorze $\mathbb{R}$, więc należy rozważyć cztery obszary: $ x\in]-\infty;-4[$, $ x\in]-4;0[$, $ x\in]0;4[$, $ x\in]4;\infty[$, dla których $ f$ będzie miała różne funkcje odwrotne..png)
$$
(x^2-16)^2=y \Rightarrow x^2-16=\pm\sqrt{y} \Rightarrow x^2=\pm\sqrt{y}+16,
$$
gdzie znak $ +$ otrzymujemy dla przypadków $ x^2-16>0$ $\left( x\in]-\infty;-4[$, $ x\in]4;\infty[)\right$, a znak $ -$ dla $ x^2-16 < 0$ $\left( x\in]-4;0[$, $ x\in]0;4[)\right$. Dokańczając obliczenia: $$ g(y)=\pm\sqrt{\pm\sqrt{y}+16} \\ \Rightarrow g(y) = \left\{ \begin{array}{ll} -\sqrt{\sqrt{y}+16} & \textrm{gdy $x\in]-\infty;-4[$}\\ -\sqrt{-\sqrt{y}+16} & \textrm{gdy $x\in]-4;0[$}\\ \sqrt{-\sqrt{y}+16} & \textrm{gdy $x\in]0;4[$}\\ \sqrt{\sqrt{y}+16} & \textrm{gdy $x\in]4;\infty[$} \end{array} \right. $$ Powyższy zapis należy rozumieć w taki sposób: gdy znamy przedział $ x$, z których otrzymujemy $ y$ to wtedy możemy jednoznacznie wybrać funkcję odwrotną. Nie wiedząc z jakiego przedziału pochodzi $ x$, to mając $ y$ otrzymamy kilka propozycji odpowiadającym mu $ x$-om.
Tak poskładaną "funkcję" odwrotną przedstawia rysunek poniżej.
.png)
Warto zauważyć, że dla niektórych funkcji nie jesteśmy w stanie podać jawnego wyrażenia na funkcję odwrotną np: $ f(x)=x \exp(-x),$ która jest bijekcją na przedziałach $ x\in]-\infty,1[$
oraz $ x\in]1;\infty[$.Przykład 2
Na początek wybierzmy prosty przykład: $$ f(x,y): \begin{bmatrix} x\\ y \end{bmatrix}\longmapsto \begin{bmatrix} z_1 \\ z_2 \end{bmatrix}=\begin{bmatrix}x^2+2y x\\ y-4x \end{bmatrix} $$ Licząc pochodną powyższej funkcji otrzymujemy: $$ f'(x,y)=\left( \begin{array}{cc} 2 x & 2 \\ -4 & 1 \\ \end{array} \right) $$ Łatwo zobaczyć, że wyznacznik tej macierzy wynosi: $ \det f'(x,y)=8+2x$, który oczywiście zeruje się na prostej $ x=-4$. Rzeczona prosta dzieli naszą płaszczyznę na dwie części, na których mamy dwa różne rozwiązania. Rozwiązując układ równań otrzymujemy wyrażenie na funkcję odwrotną $ g(z_1,z_2)$: $$ g(z_1,z_2) = \left\{ \begin{array}{ll} \begin{bmatrix}-\sqrt{z_1-2 z_2+16}-4\\ -4 \sqrt{z_1-2 z_2+16}+z_2-16 \end{bmatrix} & \textrm{gdy $x\in]-\infty;-4[$ , $y\in \mathbb{R}$}\\ \\ \begin{bmatrix}\sqrt{z_1-2 z_2+16}-4 \\ 4 \sqrt{z_1-2 z_2+16}+z_2-16 \end{bmatrix} & \textrm{gdy $x\in]-4;\infty[$, $y\in \mathbb{R}$ } \end{array} \right. $$ Przypomnijmy, że powyższy zapis należy rozumieć w sposób analogiczny do tego z Przykładu 1.Przykład 3
Zmodyfikujmy naszą funkcję podnosząc wyrażenie w drugim argumencie do kwadratu: $$ f(x,y): \begin{bmatrix} x\\ y \end{bmatrix}\longmapsto \begin{bmatrix} z_1=x^2+2y\\ z_2=(y-4x)^2 \end{bmatrix} $$ Tak jak poprzednio liczymy pochodną i wyznacznik: $$ f'(x,y)= \left( \begin{array}{cc} 2 x & 2 \\ -8 (y-4 x) & 2 (y-4 x) \\ \end{array} \right)\\ \det f'(x,y)=4x(-4x+y)+16(-4x+y)=4(-4x+y)(x+4) $$ Teraz widać, że otrzymamy cztery obszary o różnych rozwiązaniach. Obszary te pokazano na rysunku poniżej.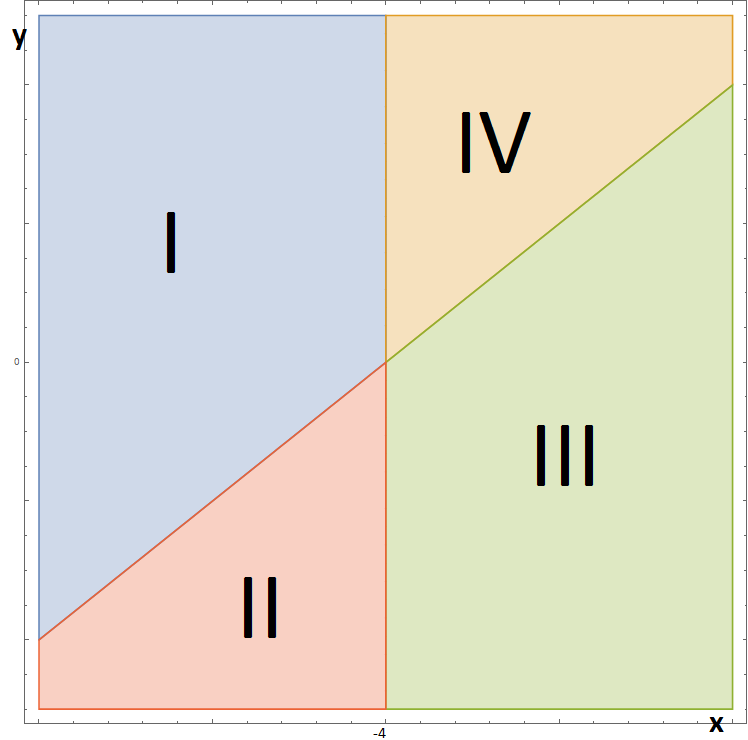
Rozwiązując układ równań na funkcję odwrotną otrzymujemy:
$$
g(z_1,z_2)= \left\{ \begin{array}{ll}
\begin{bmatrix}-\sqrt{-2 \sqrt{z_2}+z_1+16}-4\\
-4 \sqrt{-2 \sqrt{z_2}+z_1+16}+\sqrt{z_2}-16 \end{bmatrix} & \textrm{obszar I }\\
\\
\begin{bmatrix}\sqrt{-2 \sqrt{z_2}+z_1+16}-4 \\
4 \sqrt{-2 \sqrt{z_2}+z_1+16}+\sqrt{z_2}-16\end{bmatrix} & \textrm{obszar II }\\
\\
\begin{bmatrix}-\sqrt{2 \sqrt{z_2}+z_1+16}-4 \\
-4 \sqrt{2 \sqrt{z_2}+z_1+16}-\sqrt{z_2}-16 \end{bmatrix} & \textrm{obszar III }\\
\\
\begin{bmatrix}\sqrt{2 \sqrt{z_2}+z_1+16}-4 \\
4 \sqrt{2 \sqrt{z_2}+z_1+16}-\sqrt{z_2}-16\end{bmatrix}& \textrm{obszar IV}
\\
\end{array} \right.
$$
Na każdy obszar pokazany na rysunku przypada osobna funkcja odwrotna.