TWIERDZENIE O LOKALNEJ ODWRACALNOŚCI
Już tutaj warto zauważyć, że w nazwie twierdzenia jest słowo klucz: "lokalnej". Widać, że nie rozwiąże ono naszego problemu w całej przestrzeni, ale lokalna wersja często wystarcza.
1. Założenia
Zobaczmy więc jak wyglądają założenia twierdzenia o lokalnej odwracalności:
- $f$: $E\subset{\mathbb{R}^n}\rightarrow E\subset{\mathbb{R}^n}$,
- $f$ jest różniczkowalna w sposób ciągły,
- $\exists_{x_0\in{}E}$, takie, że $\exists_{y_0\in{}E}~ f(x_0)=y_0$,
- $f'(x_0)$ jest odwracalne.
Drugie założenie oznacza, że pochodna funkcji $f$ jest ciągła. Trzecie założenie jest po to, aby wykluczyć sytuację, w której $E=\emptyset$. Przy czwartym założeniu trzeba pamiętać, że $f'(x_0)$ jest . Natomiast informacja o odwracalności mówi tyle, że istnieje macierz odwrotna do macierzy $f'(x_0)$. Wynika z tego, że macierz pochodnych jest niezdegenerowana, czyli jedną z jej własności jest to, że ma wyznacznik różny od zera ($\det(f'(x_0))\neq0$).
2. Teza
- $\exists_{U,V\subset E}$ takie, że $U$ i $V$ otwarte, $x_0\in U$, $V=f(U)$ oraz $f$ jest bijekcją między $U$ i $V$.
- Istnieje funkcja $g: V \rightarrow U$ taka, że $\forall_{x\subset U}~g(f(x))=x$ oraz $g$ jest ciągła i różniczkowalna na $V$.
Z tezy wynika, że twierdzenie o lokalnej odwracalności mówi nie tylko o istnieniu funkcji $g$, ale informuje też o jej różniczkowalności. Czyli mamy coś więcej niż samo istnienie funkcji odwrotnej.
Cały cud związany z tym twierdzeniem polega na tym, że z własności funkcji w tylko jednym punkcie można wnioskować o jej własnościach na pewnym zbiorze.
3. Dowód
3.1 Istnienie $U$ i $V$ oraz bijekcja między nimi
Na początek wprowadźmy stałą $\lambda \in \mathbb{R}$ taką, że $2\lambda{}\|f'(x_0)^{-1}\|=1$. Korzystamy tutaj z odwracalności $f'(x_0)$, która jest macierzą, więc jest jakimś operatorem liniowym. Macierz odwrotna również jest operatorem liniowym i poprzez jej definiujemy stałą $\lambda$. Warto też podkreślić, że własność odwracalności pochodnej mamy tylko w jednym punkcie - $x_0$.
Z założenia wiemy, że $f'$ jest ciągłe na $E$, możemy więc napisać (definicja ciągłości):
$$ \forall_{x_c\in E}~\forall_{\varepsilon>0}~\exists_{\delta>0}~\forall_{x\in E}~\|x-x_c\|<\delta \Rightarrow \|f'(x)-f'(x_c)\|<\varepsilon. $$ Weźmy $x_c=x_0$: $$ \forall_{\varepsilon>0}~\exists_{\delta>0}~\forall_{x\in E}~\|x-x_0\|<\delta \Rightarrow \|f'(x)-f'(x_0)\|<\varepsilon. $$Zatem dla $\varepsilon=\lambda$:
$$ \forall_{x\in K(x_0,\delta)}~\|f'(x)-f'(x_0)\|<\lambda. \qquad \qquad \text{(1)} \label{def_ciaglosc} $$Weźmy teraz dowolny zbiór, który wraz ze swoim domknięciem, zawieraja się w $K(x_0,\delta)$, taki, że $x_0$ należy do tego zbioru. To będzie nasz zbiór $U$. Da się to zrobić zawsze, bo wiemy, że $\delta\neq 0$.
Następnie zdefiniujmy $V$ jako obraz $U: V=f(U)$. Taki zbiór istnieje i na pewno nie jest pusty, gdyż istnieje $y_0$ (z założenia), które musi się znajdować w $V$, bo jest obrazem $x_0$. Jednak samo istnienie zbiorów $U$ i $V$ nam nie wystarcza. My żądamy, aby $f$ była bijekcją między nimi.
Chcemy, aby:
$$ \forall_{y\in V}~\exists!_{x\in U}~ y=f(x). $$W tym miejscu musimy wprowadzić funkcję pomocniczą:
$$ \varphi_y: E\rightarrow \mathbb{R}^n $$ $$ \varphi_y(x)=x+(f'(x_0)^{-1})(y-f(x)). \qquad \qquad \text{(2)} $$W tej funkcji $y$ jest jedynie parametrem, który możemy ustalić dowolnie, nie jest on zależny od $x$.
Warto doprecyzować, że interesują nas jedynie $x\in U$ i $y\in V$. Wiemy, że dla każdego ustalonego $y\in V$ znajdziemy $x\in U$ (nazwijmy go tutaj $x_y$) takie, że $f(x_y)=y$. Dzięki zdefiniowaniu $V$ jako obrazu $U$ w odwzorowaniu $f$, mamy pewność, że znajdziemy taki $x_y$, nie wiemy natomiast, czy jest to jednoznaczne. Może dla jakiegoś $y\in V$ dałoby się znaleźć dwa punkty $x_{y}$ i $x'_{y}$, takie że $f(x_{y})=f(x'_{y})=y$? Chcielibyśmy uniknąć takiej sytuacji i dalsze rozważania mają na celu wykluczenie tej opcji.
Zauważmy że jeśli $f(x_y)=y$ to:
$$ 0=(f'(x_0)^{-1})(y-f(x_y))=x_y+(f'(x_0)^{-1})(y-f(x_y))-x_y=\varphi_y(x_y)-x_y=0. $$Jako, że w powyższych rachunkach są same równości możemy napisać:
$$ \varphi_y(x_y)=x_y \Leftrightarrow f(x_y)=y. \qquad\qquad \text{(3)} $$Wynika z tego, że dla $x_y$ odwzorowania $\varphi_y$ zachodzi $f(x_y)=y$.
Rozważmy tutaj, co by było, gdyby $\varphi_y$ było W takim wypadku (odwzorowanie zwężające ma tylko jeden punkt stały), na podstawie równania (3), dla każdego $y$ istniałby tylko jeden taki $x_y$, że $f(x_y)=y$. Pokazałoby nam to, że funkcja $f$ jest 1 do 1 między zbiorami $U$ i $V$.
Teraz udowodnijmy, że $\varphi_y$ jest odwzorowaniem zwężającym. Rozważmy odwzorowanie $\varphi_y$ dla $x\in \overline{U}$ i $y\in V$. Zaraz wyjaśnimy dlaczego potrzebujemy domknięcia zbioru $U$.
Obliczmy:
$$ \varphi_y'(x)=1+f'(x_0)^{-1}(-f'(x))=f'(x_0)^{-1}(f'(x_0)-f'(x)), $$więc pamiętając o (1):
$$ \|\varphi_y'(x)\|\le \|f'(x_0)^{-1}\|\cdot\|f'(x_0)-f'(x)\|\le \frac{1}{2 \lambda}\lambda=\frac{1}{2}. $$
Na podstawie lematu zastosowanego do funkcji $\varphi_x$ na , wiemy, że skoro $\|\varphi'_y(x)\|\le\frac{1}{2}$, to:
$$ \forall_{x,x'\in K(x_0,\delta)}~\|\varphi_y(x)-\varphi_y(x')\|\le \frac{1}{2} \|x-x'\|, $$czyli w szczególności $\overline{U}\subset K(x_0,\delta)$:
$$ \forall_{x,x'\in \overline{U}}~\|\varphi_y(x)-\varphi_y(x')\|\le \frac{1}{2} \|x-x'\|. \qquad \qquad \text{(4)} $$Wiemy więc, że $\varphi_y$ jest na $\overline{U}$, więc posiada tylko jeden punkt stały, z czego wynika, że dla każdego $y\in V$ istnieje tylko jeden $x\in \overline{U}$ (wcześniej nazywany $x_y$), taki że $f(x)=y$.
W poprzednim akapicie korzystaliśmy z zasady Banacha, dzięki czemu mogliśmy powiedzieć, że odwzorowanie $\varphi_y$ ma tylko jeden punkt stały na przestrzeni $\overline{U}$.
Rozważaliśmy dopełnienie zbioru $U$, ponieważ jednym z założeń zasady Banacha jest zupełność zbioru (w przypadku $\mathbb{R}^n$ zbiór ten musi być domknięty i ograniczony),
na którym rozważamy nasze odwzorowanie zwężające. Jednak, tak naprawdę chcielibyśmy, aby zbiór $U$ był zbiorem otwartym.
Wiemy więc, że:
$$ \forall_{y\in V}~\exists!_{x\in\overline{U}}~f(x)=y, $$ oraz: $$ \forall_{y\in V}~\exists_{x\in U}~f(x)=y. $$ Pierwszy z tych napisów mamy na podstawie zasady Banacha zastosowanej dla odwzorowania zwężającego $\varphi_y$ na zbiorze $\overline{U}$. Drugi z tych napisów mamy z definicji zbioru $V$ ($V=f(U)$). Zauważmy, że w pierwszym z nich mamy informację, że istnieje tylko jeden $x$ należący do $\overline{U}$, a w drugim po prostu istnieje $x$ należący do (niedomkniętego) zbioru $U$. Skoro wiemy, że $U\subset\overline{U}$ to możemy napisać: $$ \forall_{y\in V}~\exists!_{x\in U}~f(x)=y. $$ Z tego zdania wynika, że funkcja $f$ jest 1 do 1 między zbiorami $U$ i $V$.3.2 Otwartość zbiorów $U$ i $V$
Zauważmy tutaj, że my sami wybieraliśmy zbiór $U$. Mogliśmy więc wybrać taki zbiór, który jest otwarty. Więc właściwie należy tutaj dowieść, że zbiór $V=f(U)$ jest otwarty, jeśli $U$ jest otwarty.
Weźmy dowolny punkt $x_k$ ze zbioru $U$. Weźmy takie $r$, aby otoczenie punktu $x_k$ w postaci kuli otwartej $K(x_k,r)$ było wewnątrz $U$ oraz $\overline{K(x_k,r)}\subset U$.
Chcemy pokazać, że istnieje takie otoczenie punktu $y_k\in V$ ($y_k=f(x_k)$), które zawiera się w $V$. Dlaczego wymagamy, aby również domknięcie $K(x_k,r)\in U$ będzie wyjaśnione za chwilę.Weźmy więc kulę otwartą $K(y_k,\lambda r)$. Chcemy, aby ta kula należała do $V$, jednak w tym miejscu jeszcze nie możemy być pewni czy $K(y_k,\lambda r)\subset V$. Bo gdyby ta kula zawierała się w $V$, to mielibyśmy otoczenie otwarte wokół $y_k$ (czyli wokół dowolnego punktu z $V$), które zawierałoby się w $V$. A to jest definicja otwartości. Chcemy pokazać, że: $$ \forall_{y\in K(y_k,\lambda r)}~\exists_{x\in \overline{K(x_k,r)}}~y=f(x), $$ bo z tego by wynikało, że $K(y_k,\lambda r)\subset f(\overline{K(x_k,r})$ ,więc mielibyśmy otoczenie otwarte zawierające się w $V$ wokół dowolnego punktu z $V$.
Skorzystajmy jeszcze raz z odwzorowania $\varphi_y$. Zauważmy wpierw, że oszacowanie (4) jest prawdziwe, niezależnie od wybranego $y$. Żeby jednak pokazać, że $\varphi_y$ jest odwzorowaniem zwężającym na $\overline{K(x_k,r)}$, potrzebujemy jeszcze jednej informacji.
Mianowicie, musimy wiedzieć, że dla każdego $x\in \overline{K(x_k,r)}$, $\varphi_y(x)\in \overline{K(x_k,r)}$. Przecież może się zdarzyć, że punkt stały znajdowałby się poza zbiorem $\overline{K(x_k,r)}$. Wtedy nie mielibyśmy pewności, czy $K(y_k,\lambda r)\subset V$.
Sprawdźmy więc czy $\varphi_y(x)\in \overline{K(x_k,r)}$, jeśli $y\in K(y_k,\lambda r)$ i $x\in \overline{K(x_k,r)}$, szacując:
$$ \|\varphi_y(x)-x_k\|\le \|\varphi_y(x)-\varphi_y(x_k)\|+\|\varphi_y(x_k)-x_k\|\le $$ $$ \le \frac{1}{2}\|x-x_k\|+\|f'(x_0)^{-1}\|\cdot\|y-y_k\| \le \frac{r}{2}+\frac{1}{2\lambda} \lambda r=r. $$Widać więc, że $\|\varphi_y(x)-x_k\| \le r$, zatem dla $x\in \overline{K(x_k,r)}$, oraz $y\in K(y_k, \lambda r)$, punkt stały odwzorowania $\varphi_y$ znajduje się wewnątrz kuli $\overline{K(x_k,r)}$. Czyli:
Wiemy, że dla każdego $y\in K(y_k,\lambda r)$, $\varphi_y$ jest zwężające na kuli $\overline{K(x_k,r)}$, czyli punkt stały tego odwzorowania znajduje się wewnątrz zbioru $\overline{K(x_k,r)}$ i jest tylko jeden. Pamiętając o (3), możemy napisać:
$$ \forall_{y\in K(y_k,\lambda r)}~\exists!_{x\in \overline{K(x_k,r)}} ~y=f(x). \qquad\qquad\text{(5)} $$W tym miejscu rozumowania istotne było to, że rozważaliśmy domknięcie $K(x_k,r)$. Korzystaliśmy tutaj z zasady Banacha, dzięki której wiemy, że punkt stały istnieje i jest tylko jeden. Jednak wymagają, aby zbiór, na którym rozważamy nasze odwzorowanie, był zupełny. W przestrzeniach $\mathbb{R}^n$ zbiór zupełny to zbiór domknięty i ograniczony, co nie jest spełnione przez $K(x_k,r)$, ale przez $\overline{K(x_k,r)}$ już tak.
Z (5) wynika, że $K(y_k,\lambda r)\subset f(\overline{K(x_k,r)})\subset V$, a więc dla każdego punktu z $V$ istnieje otoczenie otwarte zawierające się w $V$, czyli $V$ jest otwarty.
3.3 Funkcja $g$
W tej części przyda nam się informacja, że $f'(x)$ jest odwracalne nie tylko w punkcie $x_0$, ale również dla każdego $x\in U$. Jednak założenia mówią jedynie o odwracalności w punkcie $x_0$. Musimy więc pokazać, że ta własność rozciąga się na inne punkty należące do $U$.
W tym celu, dla dowolnego wektora $w$, oszacujmy:
$$ 0\le \frac{1}{\|f'(x_0)^{-1}\|}\|w\|\le \frac{1}{\|f'(x_0)^{-1}\|}\|(f'(x_0)^{-1})f'(x_0)w\|\le \|f'(x_0)w\|= $$ $$ =\|(f'(x_0)-f'(x)+f'(x))w\|\le \|f'(x_0)-f'(x)\|\cdot\|w\|+\|f'(x)w\|\le \notag\\ \le \lambda\|w\|+\|f'(x)w\|\le \frac{1}{2\|f'(x_0)^{-1}\|}\|w\|+\|f'(x)w\| $$ Korzystaliśmy tutaj z (1). Zatem mamy: \begin{eqnarray} \frac{1}{\|f'(x_0)^{-1}\|}\|w\|&\le&\frac{1}{2\|f'(x_0)^{-1}\|}\|w\|+\|f'(x)w\| \nonumber \\ \\ \frac{1}{2\|f'(x_0)^{-1}\|}\|w\|&\le&\|f'(x)w\|, \nonumber \end{eqnarray} ale wiemy, że z definicji normy wyrażenie $\frac{1}{2\|f'(x_0)^{-1}\|}\|w\|$ jest większe lub równe 0, czyli: $$ 0\le \frac{\|w\|}{2\|f'(x_0)^{-1}\|}\le \|f'(x)w\|. $$Warto również zauważyć, że powyższe wyrażenie ma szansę być równe zero jedynie w przypadku, gdy $w=0$. Możemy więc zmienić nierówność na jej ostrą wersję jeśli narzucimy warunek, że $w\neq 0$.
Wiemy zatem, że:
$$ \forall_{x\in U}~\forall_{w\neq 0, w\in E}~\|f'(x)w\|>0, $$Oznacza to, że $f'(x)$ jest odwracalne dla każdego $x\in U$. Ze znalezionej nierówności wynika, że $f'(x)w=0$ jedynie wtedy gdy $w=0$, a jest to własność, którą posiadają tylko macierze odwracalne.
Zauważmy teraz, że skoro funkcja $f$ jest bijekcją między zbiorami $U$ i $V$, to istnieje funkcja $g$, która jest funkcją odwrotną do $f$. Musimy więc tylko udowodnić, że jest ona różniczkowalna. Przy okazji pokażemy ciągłość funkcji $g$, bo funkcja różniczkowalna musi być ciągła.
Rozważmy punkt $x\in U$, który jest przesunięty o wektor $h$, taki że $(x+h)\in U$.
Wtedy punkt $y=f(x)\in V$ przesunie się o wektor $k$, tak że $(y+k)=f(x+h)\in V$, czyli $k=f(x+h)-f(x)$. Chcielibyśmy znaleźć jakąś zależność między $k$ i $h$.Obliczmy teraz:
$$ \varphi_y(x+h)-\varphi_y(x)=x+h-x-f'(x_0)^{-1}(f(x+h)-f(x))=h-f'(x_0)^{-1}k. $$Zatem (wiedząc, że $\varphi_y$ jest zwężające):
$$ \|\varphi_y(x+h)-\varphi_y(x)\|=\|h-f'(x_0)^{-1}k\|\le \frac{1}{2}\|h\| $$ $$ \frac{1}{2}\|h\|\ge \|h-f'(x_0)^{-1}k\|\ge \|h\|-\|f'(x_0)^{-1}k\|$$z czego wynika, że:
$$ \frac{1}{2} \|h\|\le\|f'(x_0)^{-1}k\|\le\|f'(x_0)^{-1}\|\cdot\|k\|=\frac{\|k\|}{2}\lambda. $$Otrzymujemy więc oszacowanie:
$$\|k\|\ge \lambda \|h\| \qquad\qquad \text{(6)}$$Ta nierówność pozwala nam stwierdzić, że jeśli będziemy zbiegać z $k\rightarrow 0$, to również $h\rightarrow 0$.
Reszta z dla funkcji $g$ wygląda tak: $$r(y,k)=g(y+k)-g(y)-g'(y)k.$$
Możemy sprawdzić co by było gdyby $g'(y)=f'(x)^{-1}$. Wtedy reszta przyjęłaby postać: $$r(y,k)=g(y+k)-g(y)-f'(x)^{-1}k$$.
Jeśli uda się nam pokazać, że tak zdefiniowana reszta dla funkcji $g$ dąży odpowiednio szybko do zera, to będzie z tego wynikało, że $g'(y)=f'(x)^{-1}$. Czyli otrzymamy nie tylko fakt różniczkowalności funkcji $g$, ale również poznamy dokładną postać jej pochodnej.
Zatem:
$$ r(y,k)=g(y+k)-g(y)-f'(x)^{-1}k=x+h-x-f'(x)^{-1}k=h-f'(x)^{-1}k= $$ $$ =f'(x)^{-1}(f'(x)h-k)=f'(x)^{-1}(f'(x)h+f(x)-f(x+h)). $$Pokażemy teraz, że:
$$ \frac{\|r(y,k)\|}{\|k\|}\xrightarrow{k\to 0} 0. $$Jeśli nam się to uda, to udowodnimy, że $r(y,k)$ faktycznie jest dobrą resztą, a co za tym idzie, założona postać pochodnej funkcji $g$ jest poprawna. Skorzystamy z faktu, że reszta dla funkcji $f$ spełnia:
$$ \frac{\|r(x,h)\|}{\|h\|}\xrightarrow{h\to 0} 0. \qquad\qquad\text{(7)} $$A więc:
$$ \frac{\|f'(x)^{-1}\|\cdot\|f(x+h)-f(x)-f'(x)h\|}{\|k\|}\le \frac{\|f'(x)^{-1}\|\cdot\|f(x+h)-f(x)-f'(x)h\|}{\lambda \|h\|}\le $$ $$ \le\frac{\|f'(x)^{-1}\|}{\lambda}\frac{\|r(x,h)\|}{\|h\|}\xrightarrow[h\to 0]{k\to 0} 0 $$Skorzystaliśmy tutaj z oszacowania (6), dzięki któremu wiedzieliśmy, że jeśli $k\to 0$ to $h\to 0$. Wiemy, że reszta dla funkcji $f$ spełnia (7), więc musi odpowiednio szybko zbiegać do zera. Dodatkowo $\frac{\|f'(x)^{-1}\|}{\lambda}<\infty$, więc pomnożenie czegoś zbiegającego do zera przez ten czynnik niczego nie psuje.
Udało nam się ostatecznie udowodnić, że $g$ również jest różniczkowalna, a więc i ciągła. Co więcej wiemy dokładnie jak wygląda jej pochodna w dowolnym punkcie należącym do $V$, gdzie $y=f(x)$. Mianowicie:
$$ g'(y)=f'(x)^{-1}. $$$ \square$
Zachęcamy teraz czytelnika do ponownego zapoznania się z przykładami.png) $$\Large
(x^2-16)^2=y \Rightarrow x^2-16=\pm\sqrt{y} \Rightarrow x^2=\pm\sqrt{y}+16,
$$
gdzie znak $\Large +$ otrzymujemy dla przypadków $\Large x^2-16>0$ $\Large\left( x\in]-\infty;-4[\text{, } x\in]4;\infty[\right)$,
$$\Large
(x^2-16)^2=y \Rightarrow x^2-16=\pm\sqrt{y} \Rightarrow x^2=\pm\sqrt{y}+16,
$$
gdzie znak $\Large +$ otrzymujemy dla przypadków $\Large x^2-16>0$ $\Large\left( x\in]-\infty;-4[\text{, } x\in]4;\infty[\right)$, .png) Warto zauważyć, że dla niektórych funkcji nie jesteśmy w stanie podać jawnego wyrażenia na funkcję odwrotną np: $\Large f(x)=x \exp(-x),$ która jest bijekcją na przedziałach $\Large x\in]-\infty,1[$
oraz $\Large x\in]1;\infty[$.
Warto zauważyć, że dla niektórych funkcji nie jesteśmy w stanie podać jawnego wyrażenia na funkcję odwrotną np: $\Large f(x)=x \exp(-x),$ która jest bijekcją na przedziałach $\Large x\in]-\infty,1[$
oraz $\Large x\in]1;\infty[$.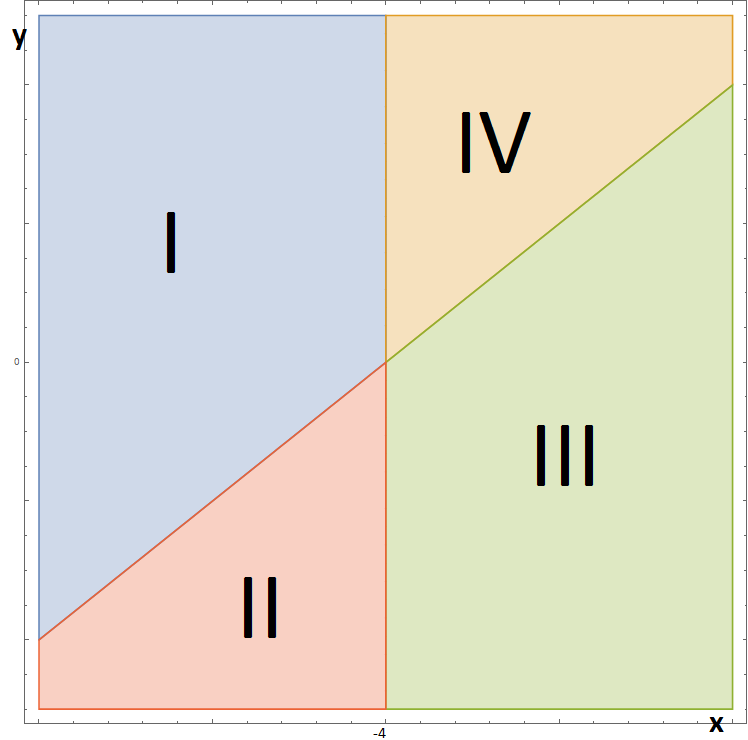 Rozwiązując układ równań na funkcję odwrotną otrzymujemy:
$$\Large
g(z_1,z_2)= \left\{ \begin{array}{ll}
\begin{bmatrix}-\sqrt{-2 \sqrt{z_2}+z_1+16}-4\\
-4 \sqrt{-2 \sqrt{z_2}+z_1+16}+\sqrt{z_2}-16 \end{bmatrix} & \textrm{obszar I }\\
\\
\begin{bmatrix}\sqrt{-2 \sqrt{z_2}+z_1+16}-4 \\
4 \sqrt{-2 \sqrt{z_2}+z_1+16}+\sqrt{z_2}-16\end{bmatrix} & \textrm{obszar II }\\
\\
\begin{bmatrix}-\sqrt{2 \sqrt{z_2}+z_1+16}-4 \\
-4 \sqrt{2 \sqrt{z_2}+z_1+16}-\sqrt{z_2}-16 \end{bmatrix} & \textrm{obszar III }\\
\\
\begin{bmatrix}\sqrt{2 \sqrt{z_2}+z_1+16}-4 \\
4 \sqrt{2 \sqrt{z_2}+z_1+16}-\sqrt{z_2}-16\end{bmatrix}& \textrm{obszar IV}
\\
\end{array} \right.
$$
Na każdy obszar pokazany na rysunku przypada osobna funkcja odwrotna.
Rozwiązując układ równań na funkcję odwrotną otrzymujemy:
$$\Large
g(z_1,z_2)= \left\{ \begin{array}{ll}
\begin{bmatrix}-\sqrt{-2 \sqrt{z_2}+z_1+16}-4\\
-4 \sqrt{-2 \sqrt{z_2}+z_1+16}+\sqrt{z_2}-16 \end{bmatrix} & \textrm{obszar I }\\
\\
\begin{bmatrix}\sqrt{-2 \sqrt{z_2}+z_1+16}-4 \\
4 \sqrt{-2 \sqrt{z_2}+z_1+16}+\sqrt{z_2}-16\end{bmatrix} & \textrm{obszar II }\\
\\
\begin{bmatrix}-\sqrt{2 \sqrt{z_2}+z_1+16}-4 \\
-4 \sqrt{2 \sqrt{z_2}+z_1+16}-\sqrt{z_2}-16 \end{bmatrix} & \textrm{obszar III }\\
\\
\begin{bmatrix}\sqrt{2 \sqrt{z_2}+z_1+16}-4 \\
4 \sqrt{2 \sqrt{z_2}+z_1+16}-\sqrt{z_2}-16\end{bmatrix}& \textrm{obszar IV}
\\
\end{array} \right.
$$
Na każdy obszar pokazany na rysunku przypada osobna funkcja odwrotna.